Master sulla trasmissione
nei modelli ferroviari (parte 1)
![]()
Master sulla trasmissione
nei modelli ferroviari (parte 1)
![]()
CENNI GENERALI SULLA TRASMISSIONE DEL MOTO
Uno dei rincipali problemi che si presenta al modellista costruttore,
è il trasmettere appropriatamente il moto dal motore elettrico
alle ruote del modello, ottenendo una opportuna forza di trazione
al modello, ma anche appropriate velocità minima e massima.
I motori elettrici generalmente hanno un numero di giri alla tensione
12 Volt, troppo elevato per le esigenze del fermodellismo, dove
si vuole, generalmente, ottenere un modello che si avvii dolcemente
e possa muoversi anche a bassissima velocità.
Senza un’adeguata riduzione del rapporto di trasmissione, anche
nell’ipotesi di applicare al motore un basso voltaggio, la velocità
di rotazione di questo resta sempre troppo elevata e la coppia
motrice trasmessa, decisamente modesta.
Siamo costretti quindi a ridurre il rapporto di trasmissione,
come detto, e questo normalmente lo si ottiene utilizzando una
cascata di ingranaggi opportunamente calcolata che, oltre a ridurre
il numero di giri alle ruote, possa anche aumentare la coppia
motrice disponibile a queste.
Nella scelta del motore elettrico, compatibilmente con lo spazio
disponibile e con i motori elettrici reperibili in commercio,
è sempre conveniente scegliere il modello che dispone di più coppia
e più potenza, dato che quest’ultima non e' mai sufficiente, unitamente
a consumi limitati e, soprattutto, al minor numero di giri possibile,
poiche' e' proprio questo l'aspetto che ci potra' agevolare molto
nell'ottenere quelle caratteristiche di marcia enumerate sopra.
Abbiamo parlato di “cascata” di ingranaggi, ma cosa si intende
con questo termine? E' molto semplice, in pratica si definisce
"cascata", l'insieme di ruote dentate, tutte connesse tra di loro,
che formano l'insieme della trasmissione del moto dall'albero
del motore a quelli delle ruote. Ma non esistono solo ingranaggi
nelle trasmissioni, molti sono i sistemi utili a trasmettere il
moto, a volte di natura ben diversa dalle ruote dentate, quindi,
credo opportuno dare un breve cenno ai vari sistemi di trasmissione
del moto, una panoramica su quelle che sono le varie tecniche
possibili e sulle leggi che le regolano; cominciamo questo cammino,
dalle più intuitive ruote di frizione che ci permettono di introdurre
concetti poi utili a comprendere meglio gli altri tipi di trasmissione,
soprattutto quella ad ingranaggi, che e' quella piu' consona alle
nostre costruzioni.
RUOTE DI FRIZIONE
Addentriamoci nella prima definizione: si dice velocità “periferica”
di una ruota, la velocità che anima i punti della periferia della
ruota stessa. Pare evidente che, quando esse funzionano correttamente,
cioè senza slittamento, esse hanno la stessa velocità nel punto
di contatto A (fig. 1).

fig. 1
Avere la medesima velocità periferica; ma con diametri diversi,
implica avere un numero di giri diverso fra le due ruote.
Il numero di giri dell’albero si esprime in “giri al minuto primo”
o in “giri al secondo (g/s)”.
Indichiamo con:
vp = il valore della velocità periferica (eguale per ambedue le
ruote);
D1 = diametro della ruota 1;
D2 = diametro della ruota 2;
n1 = velocità di rotazione della ruota 1;
n2 = velocità di rotazione della ruota 2.
Avremo che la velocità periferica sarà data dalla seguente formula:
vp = n1 x D1/2 = n2 x D2/2
Definiamo ora il rapporto di trasmissione dato da:
i = n1 / n2
e quindi essendo la velocità periferica uguale per entrambe le
ruote, abbiamo che il numero di giri è inversamente proporzionale
al diametro delle due ruote.
n1 / n2 = D2 / D1
cioè una nuova espressione di t come rapporto fra i diametri esterni delle due ruote accoppiate.
Chiaramente questa non e' tra le trasmissioni tipiche dei modelli ferroviari, ma e' stata parecchio usata nepassato in parecchie animazioni di giocattoli, in quanto, di fatto, e' molto semplice, poco costosa e l'accoppiamento tra gli assi, essendo gestito da una frizione, non e' rigido e, se la frizione avviene tra due coni che abbiano liberta' di spostamento assiale reciproco, potrebbe dar luogo anche ad un variatore continuo di velocita', naturalmente entro i limiti del rapporto minimo e massimo consentito dai diametri delle ruote impegnate.
Con questo tipo di trasmissione possiamo giocare un po' con l'angolo tra gli assi delle pulegge ed ottenere rinvii un po' particolari, anche a 90°, ma la distanza tra questi e' vincolata dal diametro delle pulegge.
TRASMISSIONE A CINGHIA
La trasmissione può avvenire per mezzo di cinghie quando i due
alberi tra i quali deve avvenire la trasmissione del moto, non
sono vicini.
Si deve perciò ricorrere ad un organo che faccia da collegamento.

fig 2
Questo particolare tipo di trasmissione puo' essere consono al nostro hobby, in quanto molto semplice e piu' volte, anche da parte di grandi Case, e' stato utilizzato.
Nella meccanica tradizionale, questo organo può essere:
1) una cinghia, piatta o trapezoidale o articolata.
2) Una catena metallica conformata opportunamente.
3) Una fune metallica.
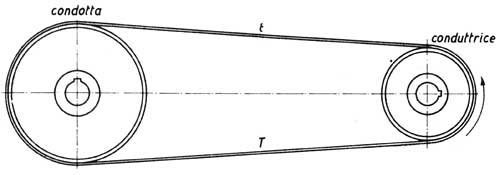
fig 3
Nel fermodellismo, invece, possiamo affidarci ad una piccola cinghia dentata, una di quelle ch si usano anche in robotica, oppure piu' semplicemente ad un ORing di adeguate dimensioni oppure addirittura ad un elastico purche' sia sempre adeguato alla potenza da trasmettere, ma vedremo nell'uso pratico che le potenze in gioco nel fermodellismo sono di livello cosi' piccolo che le dimensioni di queste cinghiette possono essere sempre molto contenute.
Una caratteristica vantaggiosa nell'uso della trasmissione a cinghia nel fermodellismo, e' quella di permetterci l'accoppiamento tra assi tra loro distanti, anche ortogonali, o, comunque, variamente disassati.
Trasmissioni con cinghia piatta.
Ma vediamo la trasmissione a cinghia nelle sue regole e nelle
sue formule meccaniche. Perche' qualche accenno a cio' che rappresenta
la trasmissione a cinghia in meccanica, ci fa capire che non e'
poi un tipo di trasmissione cosi' banale, anche se noi lo sottovalutiamo
per la sua semplicita' e per la sua intuitivita'.
La trasmissione a cinghia è rappresentata dalla figura sottostante.
E’ noto che i due tratti della cinghia risultano avere tensioni
diverse; uno è meno teso (tensione t); l’altro è più teso (tensione T).
Con buona approssimazione si ha che la differenza tra le due tensioni
è uguale allo sforzo periferico da trasmettere:
P=T-t
Generalmente i rapporti fra lo sforzo periferico e le tensioni
sono:
t=1,5 P
T=2,5 P
Quindi in base alla seguente formula della resistenza a trazione:
K= (2,5 P)/(B s)
Dove B è la larghezza della cinghia ed s lo spessore della cinghia e
K è:
per cinghia in cuoio (0,1-0,4 kg/mm2) per cinghia in gomma (0,15-0,25
kg/mm2).
Questa formula viene usata per calcolare lo spessore s, una volta fissato B.
Le due pulegge conduttrice e condotta, se si escludono slittamenti
della cinghia, hanno la stessa velocità periferica; cioè
pigreco d1 n1 = pigreco d2 n2
da cui si ricava il rapporto di trasmissione i:
i = (n1 / n2) = (d2 / d1)
la tensione della cinghia deve essere tale da garantire un’aderenza
sufficiente per la continuità della trasmissione.
Si deve infine tenere conto che, causa slittamento della cinghia
, che risulta praticamente inevitabile, si ha in genere una perdita
di giri della ruota condotta , che in genere può giungere facilmente
anche al 2% nelle trasmissioni industriali, ma ben maggiore percentualmente,
verra' ad essere in quelle modellistiche.
Per aumentare l’arco di avvolgimento della cinghia, specialmente
sulla puleggia con diametro minore, conviene l’uso del rullo avvolgitore
(fig. 4).

fig. 4
Il rullo avvolgitore, talvolta detto anche, ma erroneamente, tenditore,
deve esercitare la sua azione sul tratto meno teso della cinghia.

fig. 5
Trasmissioni con cinghia trapezoidale.
Altro sistema di trasmissione è quello con cinghia trapezoidale,
fabbricate con gomma e tela, conformate ad anello continuo senza
giunzione, montate su pulegge opportunamente scanalate.
Questo tipo di trasmissione è particolarmente diffusa per l’elevata
aderenza, dovuta sia alla natura della cinghia, sia all’effetto
cuneo che essa esercita sulla gola della puleggia.
A parità di ogni altra condizione, l’aderenza ottenibile con cinghie
trapezoidali è circa il triplo di quello di una cinghia piana.
RUOTE DENTATE
Le ruote dentate, concettualmente, non differiscono per nulla
da quelle di frizione, se non perché la loro periferia, anziché
essere liscia è fornita da una apposita dentatura, onde poter
trasmettere il moto senza slittamento fra le due ruote.
Infatti, in questo caso, la trasmissione del moto avviene non
per attrito, ma perché i vani dei denti di una ruota sono impegnati
dai denti dell’altra ruota.
In una trasmissione con ruote dentate, o di frizione, o a cinghia,
si ha egualmente proporzionalità inversa tra i diametri delle
ruote ed i rispettivi numeri di giri.
Definiamo ora altre grandezze caratteristiche di queste ruote
dentate.
Elementi fondamentali sono il numero di denti (z), il passo circonferenziale (p) e il passo diametrale (m), detto semplicemente modulo.
Il diametro primitivo è quello della circonferenza primitiva,
disegnata a tratto e punto nella fig. 6 sottostante; essa corrisponde
alla circonferenza esterna di una ruota di frizione che avesse
le stesse funzioni della ruota dentata in esame.

fig. 6
Vediamo ora nelle tabelle seguenti alcune definizioni fondamentali delle ruote dentate. Moltissime delle cose presenti non le guardera' nessuno tra quelli che seguono il nostro hobby, ma per i piu' attenti, i piu' curiosi ed anche per avere un documento di consultazione, semmai un giorno ci capitasse di avere un dubbio, ho pensato di farmi aiutare da un amico ingegnere meccanico, Marco Piranese, che ringrazio, per potervi proporre tutta una serie di tabelle, di definizioni e di dati molto tecnici, ma sicuramente molto utili per chi volesse approfondire un po' di piu' l'argomento.
Elementi caratteristici delle ruote dentate

fig 7

fig 8

fig 9

fig 10

fig 11

fig 12
Enunciate le definizioni più recenti sulle ruote e sugli ingranaggi,
si dovrebbe passare ad esporre le norme unificate sulle dentature,
la cui conoscenza risulta indispensabile per la progettazione
di una trasmissione.
Rammento, innanzittutto, che la maggior parte delle ruote è dimensionata
col sistema modulare.
Il modulo m è definito come il rapporto tra il diametro della primitiva e
il numero dei denti della ruota stessa;
il passo p è il rapporto tra la lunghezza della circonferenza primitiva
e il numero di denti; si ha quindi:
m = d / z
p = (pigreco x d) / z
p = pigreco x m
Due ruote dentate ingranano tra di loro se hanno lo stesso passo,
ossia lo stesso modulo.
La serie dei moduli per ruote dentate è stata unificata. Nella
tabella sottostante (fig 13), i moduli in grassetto sono quelli
da usare di preferenza in una progettazione meccanica, quelli
in carattere normale per quanto possibile, devono essere evitati.
In modellismo, pero', specialmente nelle scale di riproduzione
piu' piccole non e' possibile usare ingranaggi con modulo elevato,
in quanto questo imporrebbe diametri delle ruote dentate molto
grossi; nella pratica modellistica si usano ruote di diametro
molto piccolo, infatti, oltre ai moduli riportati nella seguente
tabella, per esigenze meccaniche specifiche, esistono anche altri
moduli. Nel campo del fermodellismo si usa frequentemente il modulo
0,5, ma spesso per le scale inferiori all’ HO si usano anche i
moduli 0,4 e 0,3.
La scelta del modulo piu' appropriato e' fondamentale nel momento in cui si progetta una trasmissione, in quanto, come abbiamo visto, il modulo definisce quanti denti abbia una ruota di un certo diametro, da cui si evince che a parita' di diametro, ruote con moduli diversi, avranno numero di denti diversi, quindi anche il rapporto di riduzione totale, a parita' di ingombri, variera' sensibilmente dall'utilizzo di un modulo o di un altro. Spesso noi ci troviamo in difficolta', a causa dei minimi spazi disponibili, nell'ottenere un adeguato rapporto di riduzione; la scelta di un modulo piu' piccolo e' la strada maestra per ottenere grandi risultati in spazi angusti. Infatti se volessimo ottenere un rapporto di riduzione di 40:1 usando un'unica ruota con modulo 0,5, ci troveremmo a dover fare i conti con una ruota di 20 mm di diametro (primitivo), mentre se passassimo al modulo 0,4 il diametro della ruota scenderebbe subito a 16 mm, per diventare di 12 mm con il modulo 0,3 o addirittura di 8 mm con il modulo 0,2. L'unico problema che insorge con l'utilizzo di moduli molto piccoli, e' che di pari passo deve crescere la precisione meccanica con cui dobbiamo operare, e talvolta, con scarsi mezzi tecnici a disposizione, questo non e' cosi' scontato. Con il diminuire del modulo anche l'altezza h del dente diminuisce di pari passo, imponendo quindi di minimizzare giochi e laschi fino a farli scomparire del tutto nell'utilizzo dei moduli piu' piccoli, basti pensare che il modulo 0,3 prevede denti la cui altezza e' all'incirca 0,3 mm.

fig 13
Ma torniamo a parlare di ruote dentate in senso tecnico.
Nella fig. 14 si vede un ingranaggio nella sua versione minima,
cioè l’insieme di due ruote dentate ingrananti.
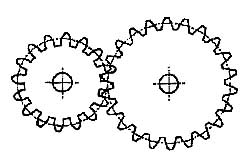
fig 14
La presenza dei denti, impedendo qualsiasi slittamento, rende
esatto ed invariabile il rapporto di trasmissione perciò le due
circonferenze primitive, tangenti fra di loro, si comportano come
due ruote di frizione esenti da slittamento.
Se la ruota motrice è quella con il minor numero di denti, mentre
quella condotta è quella con il numero di denti maggiore, applicando
le formule sopra viste notiamo che l’albero della ruota condotta
avrà un numero di giri inferiore. Ci troviamo quindi nel caso
di un ingranaggio riduttore.
Dall’osservazione della figura 14 notiamo quanto segue:
Per ingranare, due ruote dentate devono avere lo stesso modulo
p1=pigreco x d1 / z1
p2=pigreco x d2 / z2
ma, dovendo essere p1 = p2, per confronto e successiva semplificazione si ha:
pigreco x d1 / z1= pigreco x d2 / z2
Con semplici passaggi si ottiene un’ulteriore espressione di t, come rapporto fra i numeri dei denti delle due ruote, possiamo
scrivere:
i = n2 / n1 = d1 / d2 = z1 / z2
Con quest’ultima formula, dato il modulo scelto, il numero di
giri iniziale, ed il numero di giri finale scelto, possiamo trovare
il numero di denti necessario per le nostre ruote dentate.
Nel caso di forti riduzioni di numero di giri, siamo obbligati
ad usare più passaggi di riduzione, utilizzando degli alberi intermedi
di passaggio. L'utilizzo di semplici ruote cilindriche e' stato
molto usato in fermodellismo, soprattutto da Lima e da Fleischmann.
Il sistema, anche se un po' rumoroso, si rivelava robusto e reversibile,
in quanto la stessa massa volanica del motore di grande diametro,
sommata all'energia di movimento del convoglio, permettevano partenze
e fermate graduali e piacevoli. Per usare esclusivamente ruote
cilindriche l'asse di rotazione del motore sara' necessariamente
parallelo agli assi delle ruote da motorizzare.
Nella foto seguente un esempio dell'utilizzo di sole ruote cilindriche: il motore "G" della Lima.

TRASMISSIONE FRA ASSI ORTOGONALI
Se invece dobbiamo trasmettere il moto fra assi ortogonali, come
spesso accade visto che generalmente l’asse del motore elettrico
si trova parallelo all’asse della locomotiva mentre l’asse delle
ruote si trova ortogonalmente, si possono utilizzare le ruote
coniche oppure la trasmissione a vite senza fine.
RUOTE CONICHE
In fermodellismo l'uso dell'ingranaggio a ruote coniche non e'
molto usato a causa del grande controllo sui giochi e sulle tolleranze
di assemblaggio, che bisogna avere, controllo ben piu' complicato
e di difficile realizzazione rispetto all'uso di ruote dentate
cilindriche. Il grande vantaggio di questo tipo di trasmissione
e' la reversibilita', infatti, a differenza dell'accoppiamento
ruota dentata/vite senza fine, che vedremo piu' avanti, anche
qui, esattamente come nell'uso di sole ruote cilindriche visto
sopra, di fronte ad un repentino rallentamento oppure alla improvvisa
mancanza di tensione al motore, non si assistera' ad una repentina
ed innaturale frenata del modello, ma, in questi casi, sara' la
stessa energia cinetica accumulata dal modello per mezzo della
sua corsa a trasferire, invertendone la direzione, la coppia motrice
al motore che, quindi, ridurra' la sua velocita' in modo graduale
e piu' naturale. Un altro vantaggio di questa trasmissione e'
che, naturalmente, ci permette di trasferire la coppia motrice
ruotando l'asse di 90 gradi, Questo particolare ci e' molto utile
in tutti quei casi in cui l'asse del motore sia parallelo all'asse
del modello, mentre la coppia che dovremo trasferire sia trasversale
al modello. Questo tipo di accoppiamento, pero', presenta lo svantaggio
di offrire un rapporto di trasmissione molto alto, all'incirca
di 1:2, obbligando cosi' ad una cascata di ingranaggi piu' lunga,
costosa e complicata da eseguire, poiche' come noteremo nell'impiego
pratico, i modelli dovranno sfruttare, a seconda della scala,
del soggetto da riprodurre e di altri parametri specifici, un
rapporto di riduzione totale, ruote/motore che puo' variare da
20:1 fino a 60:1.
Nella foto sottostante potete vedere una applicazione di questo tipo, con accoppiamento a coppia conica e susseguente cascata di ingranaggi.

Nella realizzazione di questo tipo di riduzione e' possibile l'uso di pignone e corona non conici, ma le regole e le caratteristiche non cambiano.

Per le ruote coniche, valgono tutte le formule precedentemente
menzionate per il calcolo del rapporto di trasmissione.

fig 15
RICHIAMI CINEMATICI SULE RUOTE DENTATE CONICHE
Nelle ruote dentate coniche a denti diritti, i dati da indicare
nei disegni e per effettuare i calcoli per il rapporto di trasmissione
sono praticamente analoghi a quelle per le ruote dentate cilindriche.
Nella tabella sottostante sono rappresentati i principali dati
da utilizzare a seconda dell’angolo di incidenza fra gli assi
della ruota condotta e conduttrice.

fig 16

fig 17
INGRANAGGIO A VITE SENZA FINE
Questo tipo di trasmissione viene utilizzato quando l’asse motore
e l’asse condotto sono ortogonali, e quando il rapporto di trasmissione
abbia un valore molto piccolo. In assoluto, oggi, e' il sistema
di trasmissione del moto piu' usato da tutte le case produttrici
di modelli, per l'elevato rapporto di riduzione reso possibile
da questo meccanismo in uno spazio molto compatto e per l'assoluta
silenziosita' dell'accoppiamento.
Ecco nelle foto sottostanti due esempi di accoppiamento con moduli e rapporti di riduzione molto diversi tra loro.


La vite senza fine (fig. 18) è sempre l’elemento conduttore, la
ruota dentata è sempre l’elemento condotto, questo perché il sistema
non è reversibile. Solo in casi eccezionali di vite senza fine
con più principi, quindi con un'elica molto aperta e con scarsa
coppia trasmessa è possibile invertire il moto.

fig 18

fig 19
la vite di cui si fa uso può essere ad uno o più principi e si
comporta come una ruota avente un numero di denti uguale al numero
dei principi della vite.
Perciò, in ogni caso il rapporto di ingranaggio di questo meccanismo
è uguale a:
i = z / j
dove j è il numero dei filetti della vite e z è il numero dei denti della ruota condotta.
Nel disegno sottostante e' riprodotta la sezione di una completa trasmissione di una E424 Lima (cliccare per ingrandire)
Nella fattispecie si notera' l'esubero di ingranaggi usati in questo progetto. Se pensiamo che non si trova facilmente un ingranaggio a meno di 1,5 Euro, si notera' immediatamente l'alto costo di una trasmissione siffatta, comunque, quello che ci preme in questa sessione e' l'applicazione pratica di tutta la teoria vista precedentemente, quindi l'utilita' di questo disegno e' fuori di dubbio. In particolar modo si notera' come uno dei motivi che hanno indotto i tecnici della Lima a spostare cosi' in avanti l'accoppiamento ruota/Vite senza fine, sia il voler porre lo snodo della trasmissione esattamente sopra il punto di rotazione del carrello. Meccanicamente ineccepibile, ma nel nostro modellismo ci si puo' prendere anche qualche liberta' progettuale, come fanno anche alcune Case industriali, d'altra parte; guardate se la Mehano nel suo progetto del TGV si e' fatta qualcuno di questi scrupoli.

No, nessuno, loro sono andati dritti nella coda del carrello con
l'alberino di trasmissione, disinteressandosi del fatto che la
meccanica pretendeva soluzioni diverse e disinteressandosi anche
di dove si trovasse il centro di rotazione del carrello, sicuramente
agevolati in questo dalla lunghezza del prototipo, pero' risparmiando
in questo modo un sacco di difficolta' costruttive, un numero
notevole di componenti e un significativo tempo di manod'opera;
dulcis in fundo il modello marcia piu' che bene, liscio e silenzioso
e non da alcun problema. Nel nostro campo ci vuole "creativita’
meccanica", a volte le soluzioni semplici e geniali sono dietro
l’angolo, bisogna saper pensare nella maniera piu’ opportuna.
Le considerazioni che abbiamo fatto fin qui, ci portano a capire
come sia flessibile l'uso di questo sistema di trasmissione e
quante opportunita' ci offra facilmente e a basso costo, ma queste
riflessioni e quanto scritto piu’ sopra, non ci debbono far dimenticare
anche quelli che sono gli svantaggi insiti in questo tipo di trasmissione.
Per esempio, la non reversibilita' di questo tipo di accoppiamento
che, come abbiamo gia' visto, sottintende arresti molto repentini
nei sezionamenti e ogniqualvolta viene a mancare la tensione,
obbligando, di fatto, all'utilizzo di volani che incamerando energia
cinetica, permettano, in quei casi, un funzionamento piu' dolce
e simile al vero, omogeneizzando la marcia e le variazioni di
rotazione, rallentandone l'ascesa e allungando la discesa.
Bene, in questa prima presa di contatto con le trasmissioni del moto, abbiamo visto quella che e' la teoria e la base di cio' che riguarda le formule e la matematica applicata agli accoppiamenti. Se avremo modo, tempo e salute, un giorno passeremo ai problemi pratici, ma credo che concordiate sul fatto che la teoria avesse la precedenza, come in tutte le altre cose della vita.
Un grazie e un saluto a tutti.
Giorgio Donzello